Connectivity

To determine which parts of a graph are reachable from other parts by following the edges (respecting or ignoring their direction), connectivity algorithms can be used.

These algorithms provide functionality to check if a graph is connected, strongly connected, or biconnected. They also determine how the nodes can be distributed into two or more partitions containing only nodes that are not connected to each other. In addition, an algorithm detects the subgraphs components where each node has at least a user-specified minimum degree.

Connected Components

Colored connected components, for instance, shows a graph with two connected components.

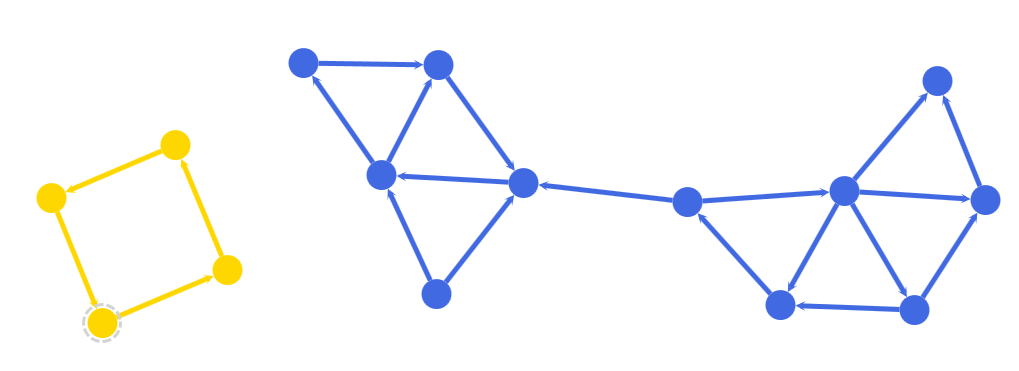
Calculating connected components and coloring the nodes and edges shows the code used to calculate the connected components and color their nodes and edges:

// calculate connected components
const connectedComponentsResult = new ConnectedComponents().run(graph)
// color the nodes and edges of each component
let colorIndex = 0
connectedComponentsResult.components.forEach((component) => {
  // get the next color from a given array of colors
  const color = colorArray[colorIndex++]

  // color the nodes
  const nodeStyle = new ShapeNodeStyle({
    shape: ShapeNodeShape.ELLIPSE,
    fill: color,
    stroke: new Stroke(color, 2)
  })
  component.nodes.forEach((node) => graph.setStyle(node, nodeStyle))

  // color the edges
  const edgeStyle = new PolylineEdgeStyle({
    stroke: new Stroke(color, 2),
    targetArrow: new Arrow({ fill: color, type: ArrowType.STEALTH })
  })
  component.inducedEdges.forEach((edge) => graph.setStyle(edge, edgeStyle))
})

Colored strongly connected components shows the same graph instance but with colored strongly connected components.

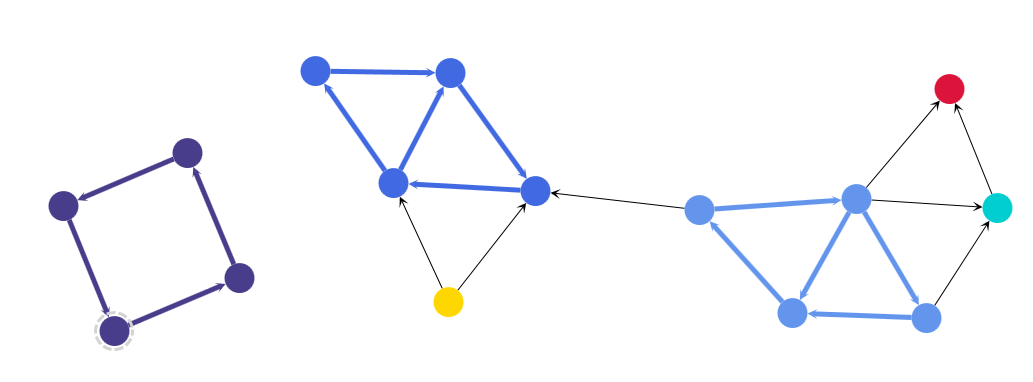
Calculating strongly connected components shows the code used to calculate the strongly connected components, which is analogous to calculating the connected components. The code coloring the nodes and edges works the same way, so it has been omitted here.

// calculate strongly connected components
const stronglyConnectedComponentsResult =
  new StronglyConnectedComponents().run(graph)

Colored biconnected components shows again the same graph instance with colored biconnected components.

Calculating biconnected components shows the analogous code used to calculate the biconnected components.

// calculate biconnected components
const biconnectedComponentsResult = new BiconnectedComponents().run(graph)

Independent Sets

The Bipartition and the more general IndependentSets algorithms calculate partitions of unconnected nodes. This can be used, for example, when entities/nodes (like employees) require limited resources (like PC workstations) and there are restrictions/edges on which entities/nodes may use the same resource (e.g., employees working at the same time).

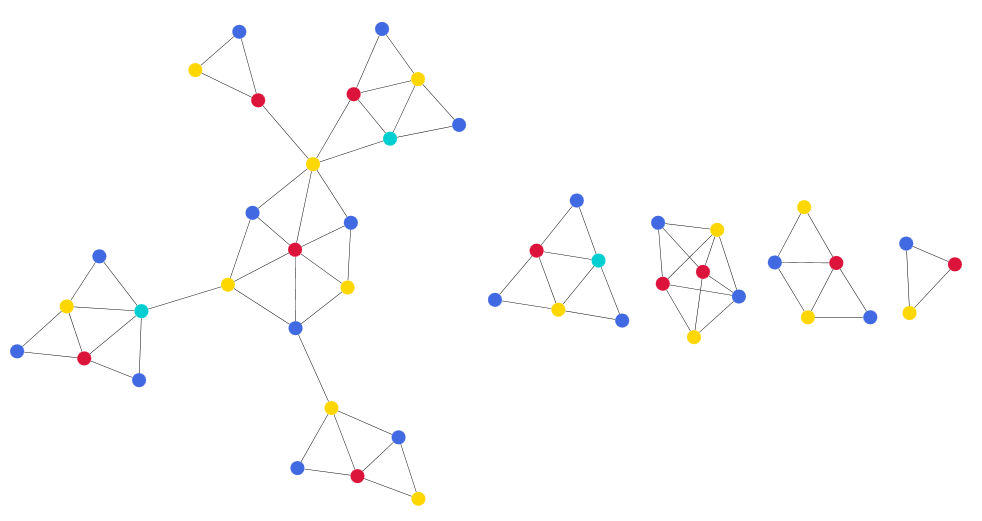
Colored independent sets shows a graph instance where each node is colored according to its set. No two adjacent nodes have the same color, and the number of colors is minimized.

Calculating Independent Sets shows the code used to calculate the independent sets.

// calculate independent sets
const independentSetsResult = new IndependentSets().run(graph)

K-Core Components

The KCoreComponents algorithm calculates the k-core of an undirected graph. The k-core consists of the subgraph components where each node has at least degree k. Note that iterating the graph and simply removing all nodes with degree less than k is not sufficient to obtain the k-core because removing a node also reduces the degree of its neighbors. Thus, a node with a degree larger than k in the initial graph may also be removed. The k-core algorithm can be applied to reduce a large graph structure to its core.

K-Core of a graph shows an example where the red colored nodes indicate the k-core of the graph for k = 3.