Centrality Measures

The importance of a single node or edge within a graph structure can be expressed using centrality measures. A centrality measure is a function that assigns a numerical value to each node or edge, representing its relative importance within the graph. The higher the value, the more important the element is considered to be.

The classes DegreeCentrality, WeightCentrality, ClosenessCentrality, GraphCentrality, PageRank, and EigenvectorCentrality provide various centrality measures for nodes. BetweennessCentrality calculates measures for both nodes and edges. Most of these algorithms can optionally take edge weights into account.

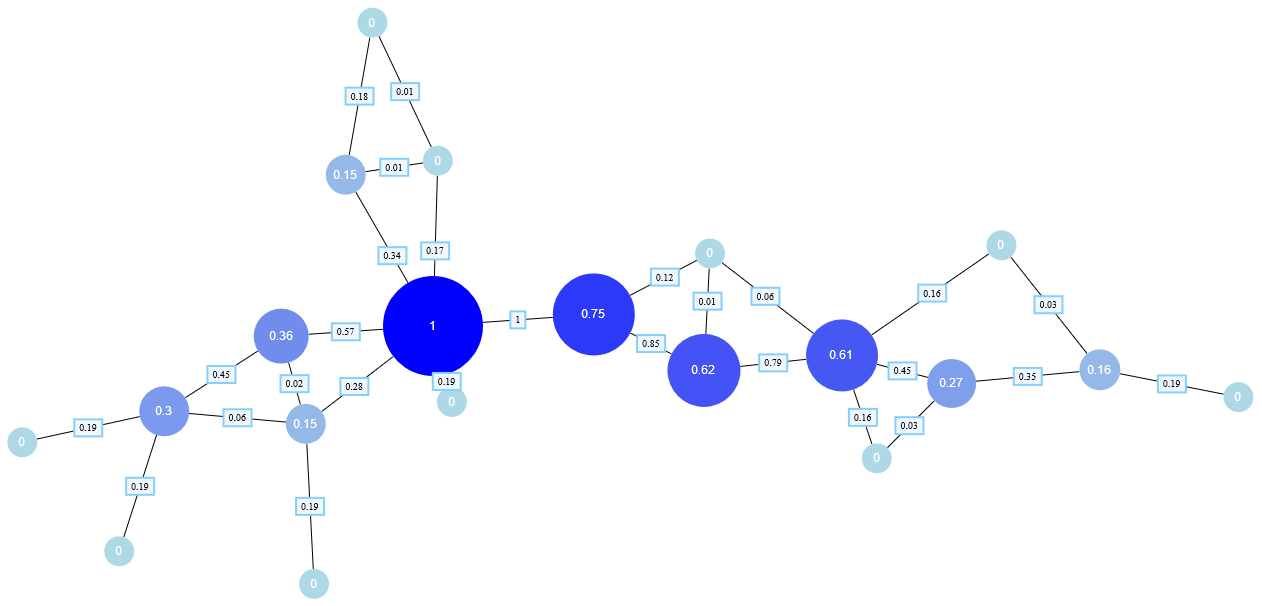
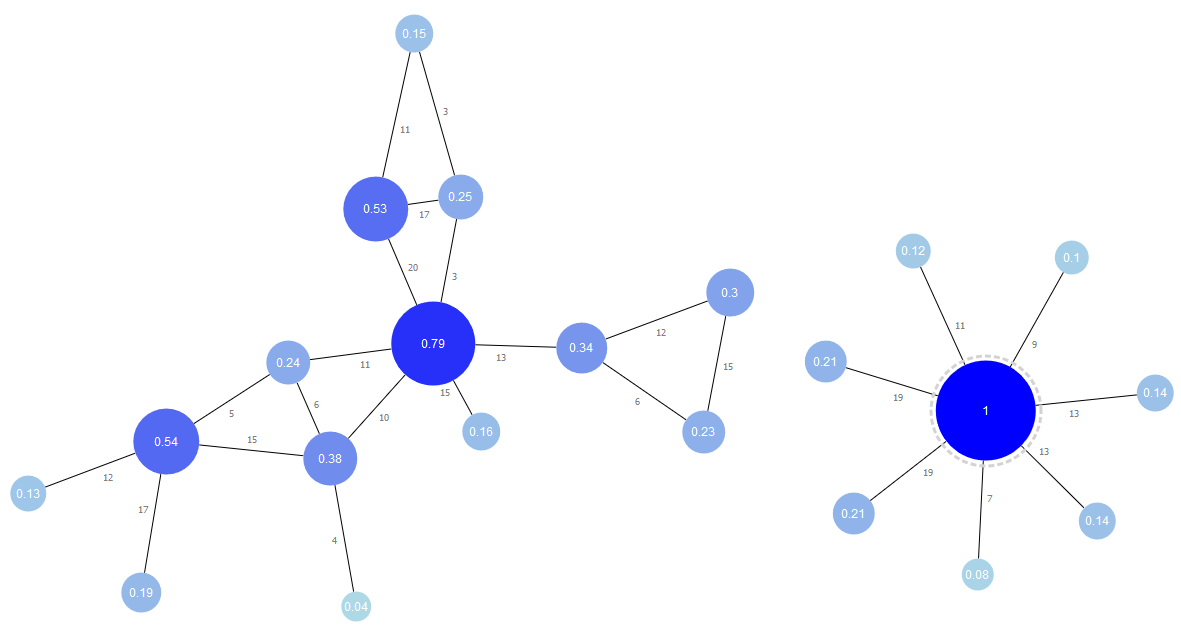
Node betweenness centrality depicts a graph with node centrality values displayed at the upper-right corner of the nodes. The numbers on the edges represent weights associated with each edge.

The centrality algorithms can be configured to either ignore or respect edge direction when computing centrality indices. DegreeCentrality and WeightCentrality can even be configured to only consider incoming edges.

The DegreeCentralityResult classes returned by the algorithms provide the centrality value for each node, as well as the minimum and maximum centrality values assigned to nodes, and a normalized centrality value that lies in the interval [0, 1].

Computing centrality indices shows the code to prepare and run the betweenness centrality algorithm on the graph depicted in Node betweenness centrality, ignoring edge directions but using edge weights.

// configure the betweenness algorithm
const betweennessCentrality = new BetweennessCentrality({
  directed: false,
  weights: (edge) => getEdgeWeight(edge)
})
// calculate the centrality values
const betweennessCentralityResult = betweennessCentrality.run(graph)

// add a label to each node that shows its normalized centrality
betweennessCentralityResult.normalizedNodeCentrality.forEach(
  (entry, centrality) => {
    graph.addLabel(
      entry.key,
      centrality.toString(),
      ExteriorNodeLabelModel.TOP_RIGHT
    )
  }
)

Closeness Centrality

Closeness centrality measures how close a node is to all other nodes in a graph. It is calculated as the reciprocal of the sum of the shortest path distances from a node to all other nodes. Therefore, a node with a high closeness centrality has short distances to all other nodes in the graph. The algorithm ClosenessCentrality supports both directed and undirected edges and optional edge weights.

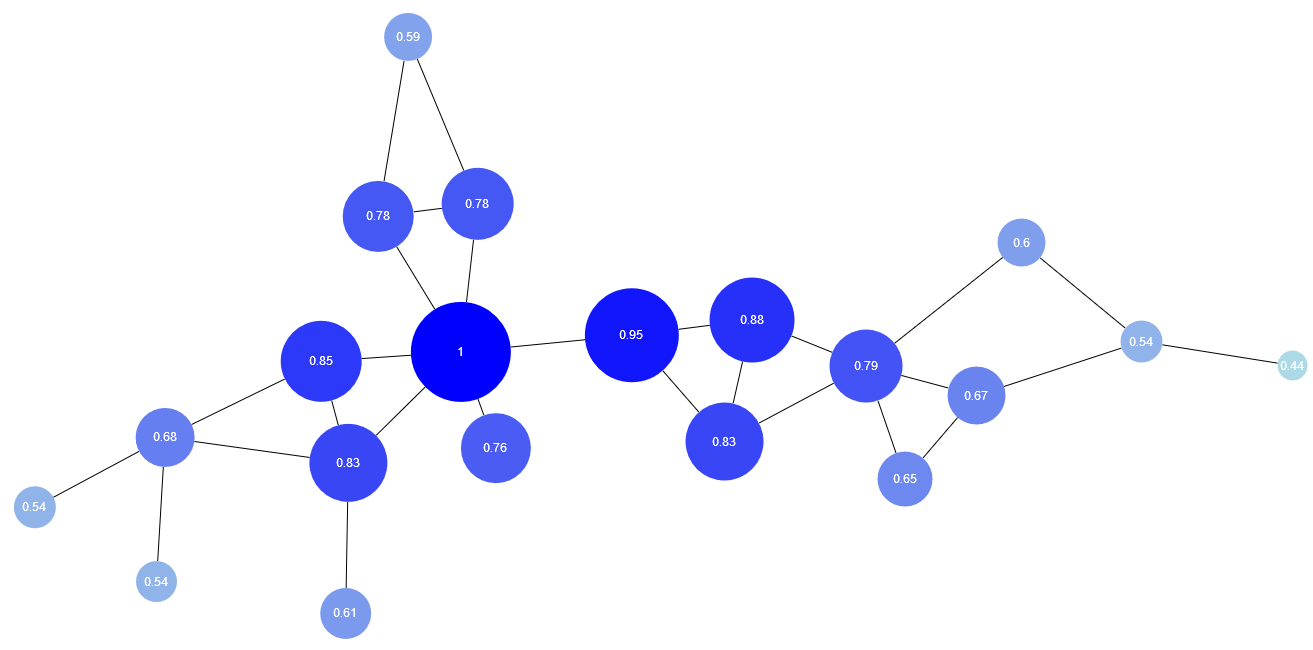
Degree Centrality

The degree centrality of a node is determined by its degree, which is the number of its incoming and outgoing edges. This value is used to determine the centrality value for each node. The DegreeCentrality algorithm can optionally be restricted to consider only incoming or outgoing edges.

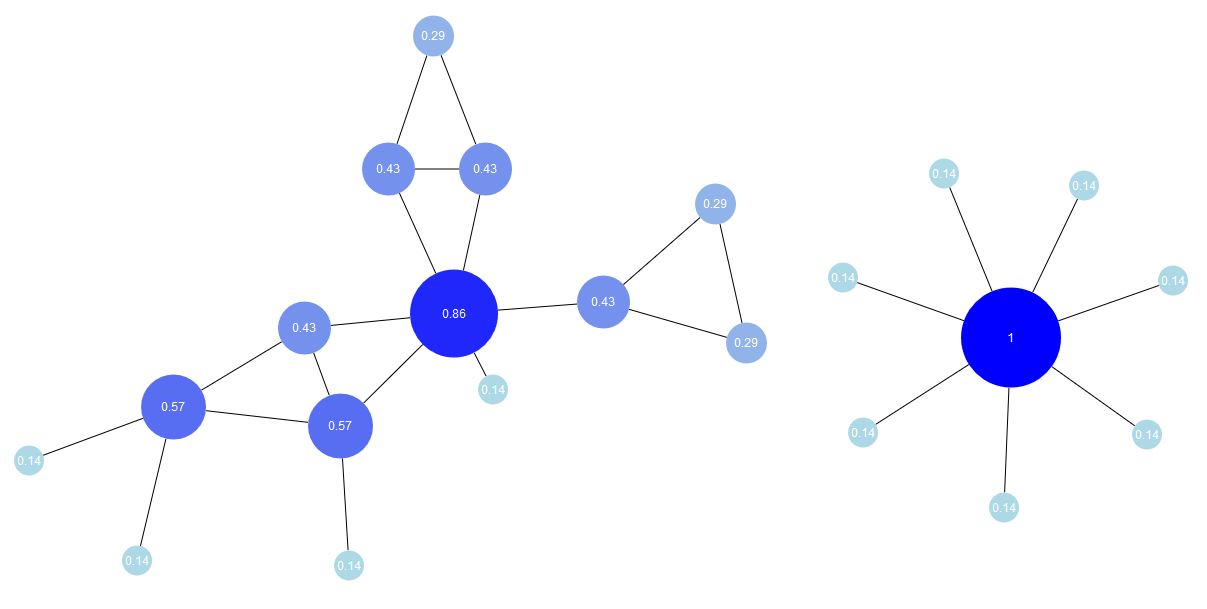
Graph Centrality

Graph centrality measures how close a node is to all other nodes in a graph. It is calculated as the reciprocal of the maximum shortest path distance from a node to all other nodes in the graph. Therefore, nodes with high graph centrality have short distances to all other nodes in the graph.

The algorithm GraphCentrality supports both directed and undirected edges and optional edge weights.

Node Edge Betweenness Centrality

Betweenness centrality measures how often a node or edge lies on a shortest path between every pair of nodes in the graph. The algorithm BetweennessCentrality supports both directed and undirected edges and optional edge weights.

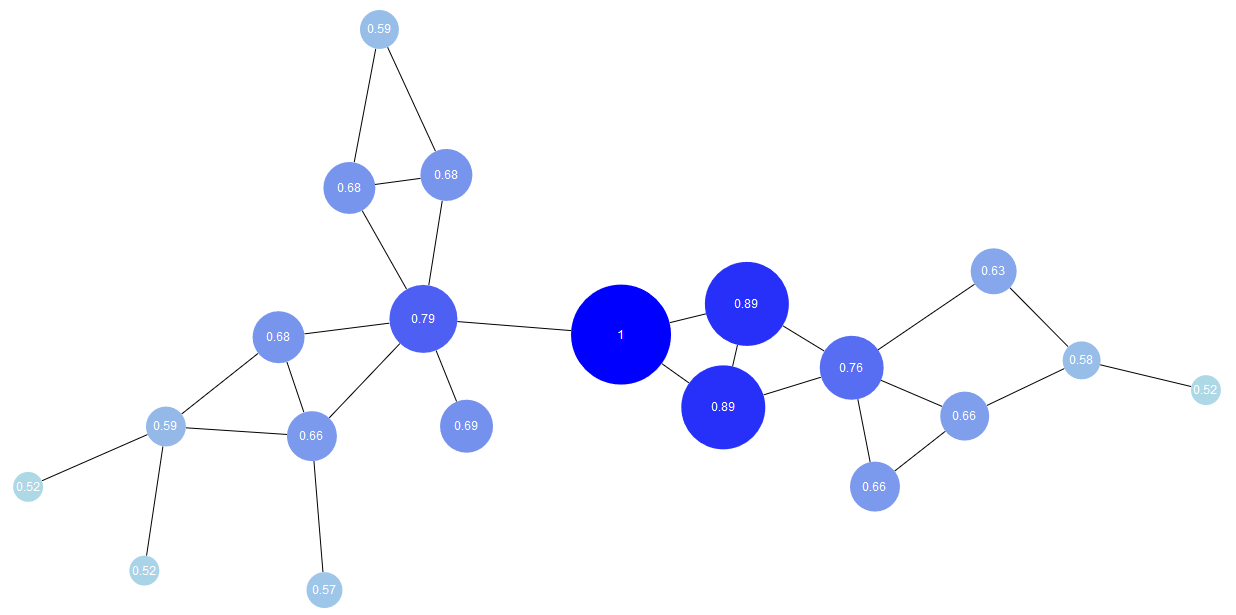
Weight Centrality

Weight centrality measures the total weight of the edges connected to a node. This can be the weight of incoming edges, outgoing edges, or all edges. When edges don’t have weights, weight centrality is the same as degree centrality. The algorithm WeightCentrality can focus on incoming or outgoing edges. It also takes edge weights into account, if they exist.

PageRank

The PageRank algorithm computes a rank value for each node in a graph, based on the graph’s edges.

The algorithm begins by assigning an initial rank value to each node. It then iteratively refines these values, propagating each node’s rank to its successors.

The algorithm PageRank supports both directed and undirected edges, as well as optional edge weights.

Eigenvector Centrality

Eigenvector centrality measures the influence of a node within a network. The more nodes that point to a given node, the higher that node’s centrality.

The EigenvectorCentrality algorithm computes the centrality for each node in a given undirected, unweighted graph.