Clustering

Clustering is the process of grouping graph elements with similar properties. The similarity measure is usually calculated based on topological criteria (e.g., the graph structure), the location of the nodes, or other characteristics (e.g., specific properties of the graph elements). Nodes that are considered similar based on this similarity value are grouped into Clusters. In other words, each cluster contains elements that share common properties and characteristics. The collection of all the clusters composes a clustering.

Cluster analysis has many application fields, such as data analysis, bioinformatics, biology, big data, business, and medicine. However, each of these applications may consider the "clustering notion" differently, which is reflected by the fact that many clustering algorithms or clustering models exist.

yFiles for HTML offers clustering algorithms using different kinds of measures.

Using a clustering algorithm

// run a clustering algorithm, in this case biconnected component clustering.
// Note that depending on the algorithm there may be additional information
// present in the result object.
const result = new BiconnectedComponentClustering().run(graph)
for (const cluster of result.clusters) {
  const nodes = cluster.nodes
  // ...
  // do something with the nodes
  // ...
}

BiconnectedComponent

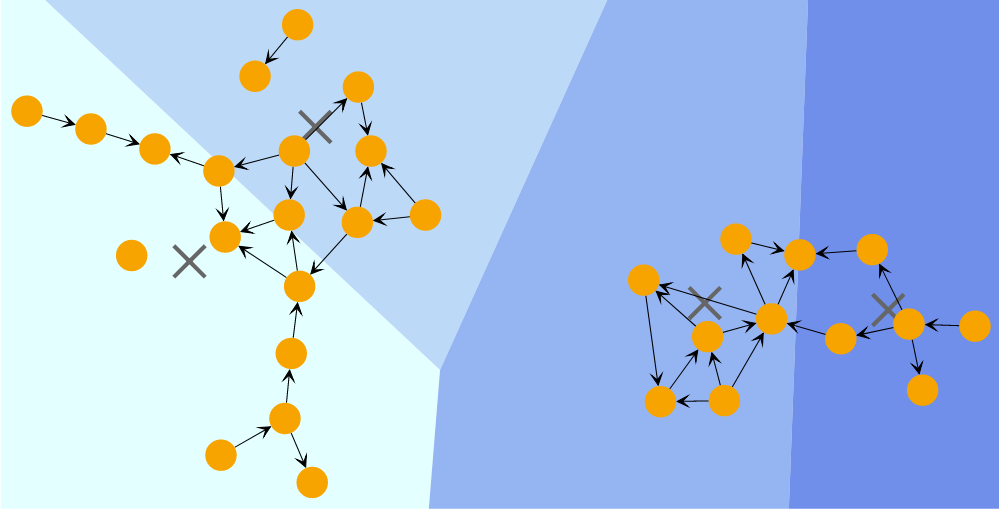
Biconnected components clustering detects clusters by analyzing the biconnected components of the graph. A biconnected component is a connected component with the property that removing any node keeps the component connected. Nodes within the same biconnected component form a cluster. If a node belongs to multiple biconnected components, the algorithm assigns it to only one of these clusters.

Biconnected Clusters shows the result of a BiconnectedComponentClustering that puts the nodes of each biconnected component in a cluster.

analysis clustering biconnected — Biconnected Clusters

KMeans

The k-Means clustering algorithm divides the graph into k clusters based on node locations. It aims to minimize the distance between each node and the mean (centroid) of its assigned cluster. This distance can be calculated using various metrics, such as Euclidean distance, squared Euclidean distance, Manhattan distance, or Chebyshev distance.

K-Means Clusters shows the result of a KMeansClustering which calculates k clusters, each consisting of a mean (or centroid) and the nodes closest to that mean.

analysis clustering kmeans — K-Means Clusters

EdgeBetweenness

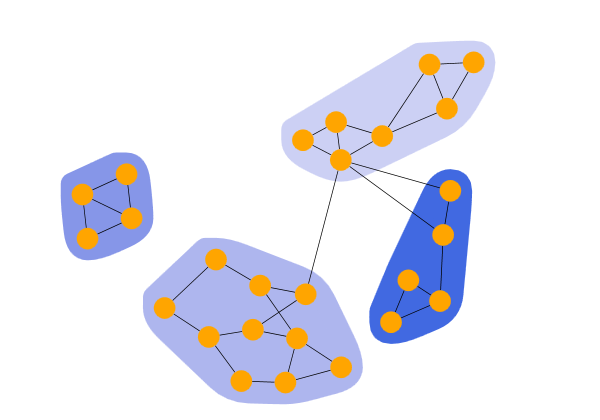
Edge Betweenness clustering identifies clusters in a graph by iteratively removing the edge with the highest betweenness centrality from the graph. Betweenness centrality measures how often a node or edge lies on the shortest path between any two nodes in the diagram. The algorithm stops when there are no more edges to remove or when it has reached the requested maximum number of clusters. The clustering result is the one that achieved the best quality during the process.

Edge-Betweenness Clusters shows the result of an EdgeBetweennessClustering with a specified clusters count of 6.

analysis clustering betweenness — Edge-Betweenness Clusters

LouvainModularity

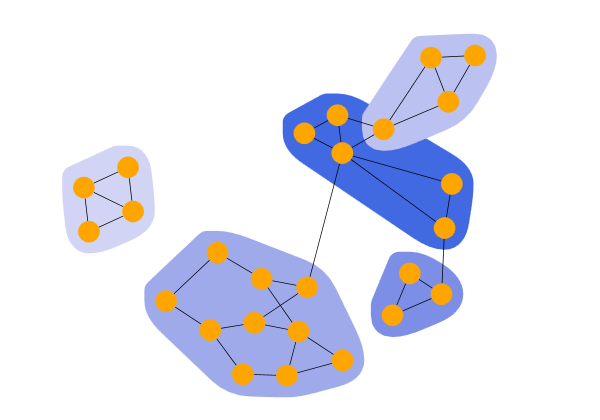
Louvain Modularity Clustering shows the result of a LouvainModularityClustering. The algorithm begins by assigning each node to its own community (or cluster). Then, it iteratively attempts to construct communities by moving nodes from their current community to another until the modularity value is locally optimized. In the next step, the smaller communities are merged into a single community, and the algorithm restarts from the beginning until the graph’s modularity can no longer be improved.

analysis clustering louvain — Louvain Modularity Clustering

LabelPropagation

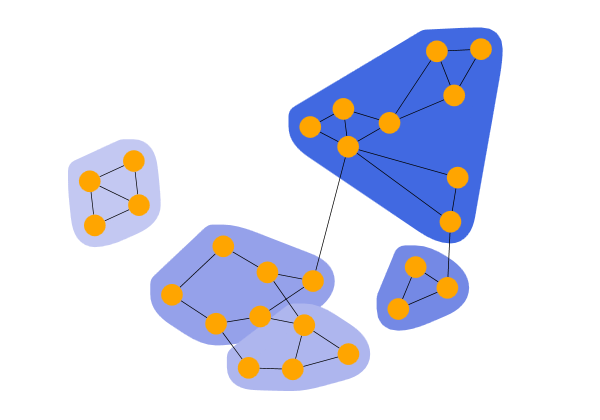
Label Propagation Clustering shows the result of a LabelPropagationClustering. The algorithm iteratively assigns a virtual label to each node. The label of a node is set to the most frequent label among its neighbors. If there are multiple candidates, the algorithm randomly chooses one. After applying the algorithm, all nodes with the same label belong to the same community or cluster.

Hierarchical

A powerful way to explore the closeness of nodes in a graph is to use the HierarchicalClustering.

The algorithm starts by assigning each node to its own cluster. It then combines the two clusters with the lowest costs into a parent cluster. The cost of combining two clusters is based on a metric that is applied to each pair of nodes from the first and second cluster, combined by the specified linkage. The result is a hierarchy of clusters where the root cluster contains all nodes.

This hierarchy offers two ways to specify which state of the algorithm to use. You can specify either the number of clusters or the cutoff. Using the cutoff value will provide only clusters that cost less than this value.

Hierarchical Clustering with different cluster counts shows clusterings of the same graph with different cluster counts.

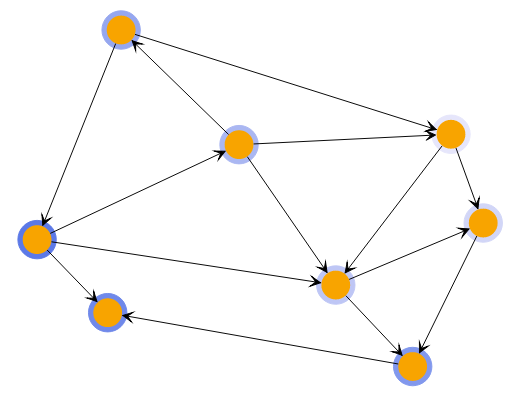
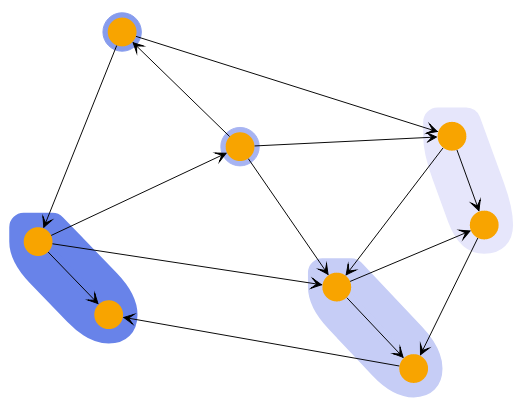
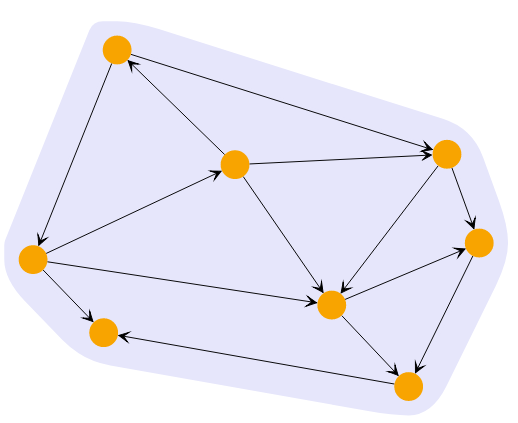
The HierarchicalClusteringResult of the HierarchicalClustering not only provides the clusters for the initially configured clusterCount or cutoff but also the methods changeClusterCount(clusterCount: number) and changeCutoff(cutoff: number) that provide new HierarchicalClusteringResults with the changed cluster count or cutoff.

The HierarchicalClusteringResult.dendrogramRoot provides access to the root of the cluster tree. The cluster tree consists of DendrogramNode, each representing one of the calculated clusters and providing access to the parent and children clusters.

Dendrogram of the hierarchical clustering shows the dendrogram of the cluster tree. A cutoff value of 110 would result in three clusters.

analysis clustering hierarchic cutoff — Dendrogram of the hierarchical clustering

Centrality Measures Connectivity